Exercise Notes

Part 1 – Algorithmic Complexity

You are running a peer-to-peer lending website that attempts to match borrowers (people who want a loan) to lenders (people who want to invest their money by lending it to someone else). You have found that as your business grows your current matching algorithm is getting too slow, so you want to find a better one. You’ve done some research and have identified a number of options:

• Option A has time complexity O(n+m) and memory complexity O(n^m) (n to the power of m)
• Option B has time complexity O(n*log(m)) and memory complexity O(n*m)
• Option C has time complexity O(n*m) and memory complexity O(n+m)

Which option do you think is most appropriate, and why? What other factors might you need to consider in making your decision?

Part 2 – Sorting Algorithms

In this module, you learnt about four sorting algorithms: Selection Sort, Insertion Sort, Merge Sort, and Quick Sort.

Build implementations of the first three sorting algorithms – Selection Sort, Insertion Sort, and Merge Sort.

• It’s fine to restrict your implementations to just sorting integers if you wish.
• Implement some tests to verify that the algorithms do actually sort the inputs correctly! Think about what the interesting test cases are.
• Run a few timed tests to check that the performance of your algorithms is as expected. For reasonably large (and therefore slow) input lists, you should find:
  • Doubling the length of the input to Selection Sort should make it run four times slower
  • If you use an already-sorted array, doubling the length of the input to Insertion Sort should make it run only twice as slowly
  • Doubling the length of the input to Merge Sort should make it run only a little worse than twice as slow. You should be able to multiply the length of the input by 10 or 100 and still see results in a little over 10 or 100 times as long.

Stretch Goal

Try repeating this for the Quick Sort algorithm.

Part 3 – Lists, Queues, and Stacks

Supermarket Shelf-Stacking Algorithm

A supermarket shelf-stacking algorithm maintains a list of products that need to be stacked onto the shelves, in order. The goal is to ensure that the shelf-stackers can work through the list efficiently while giving due priority to any short-dated items or items that are close to selling out in store. As new products arrive by lorry the algorithm inserts them into its list at an appropriate point – it doesn’t make any changes to the list other than this. What data structure implementation would you use to store the list, and why?

Comparing List Implementations

Take a look at this exercise from CodeKata. Write the three list implementations it suggests, together with some suitable tests (you could choose the test cases given as a starting point, although you’ll need to rewrite them in your preferred language). If you have time, try simplifying the boundary conditions as the kata suggests – what did you learn?

Part 4 – Searching

Comparing Search Algorithms

The file words.txt contains a long list of English words.

Write a program that loads these words into memory. Note that they’re conveniently sorted into order already.

Now implement two different search routines – one that does a linear search through this list, and one that does a binary search. Write a loop that runs 10,000 random searches on each in turn, and times the results. Prove to yourself that binary search really is a lot faster than linear search!

Stretch goal

Try this on a variety of list lengths, and graph the results. Do you see the N vs log-N performance of the two algorithms?

Sudoku

Clone the starter repo here to your machine and follow the instructions in the README to run the app.

Implement an algorithm that solves Sudoku puzzles. Use whichever depth-first or breadth-first search you think will produce the best results.

Here’s a Sudoku for you to solve:

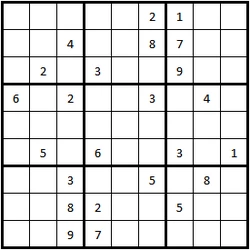
The suggested solution to this problem is to “try it and see”. So for example start with the top left cell. That cannot be 1 or 2 (already in the row), or 6 (already in the column), or 2 or 4 (already in the 3x3 square). So valid possibilities are 3, 5, 7, 8, 9. Try each of these in turn. That gives you five branches from the “root” node at the top of your search tree (i.e. the starting board). For each of these possible solutions, repeat the exercise with the next empty square, and so on. Eventually, all the search paths will lead to an impossible situation (an empty square with no valid numbers to fill it), except one. This method is sometimes called “backtracking”.

Stretch goal

Try using the other type of algorithm – depth first or breadth first – and compare the results.

Part 5 – Dictionaries and Sets

Bloom Filters

Read through the explanation of how a Bloom Filter works on CodeKata, and then implement one as suggested.

Bloom Filters by Example provides an interactive visualisation of how bloom filters work.

Find some way of testing your solution – for example generating random words as suggested in the kata, or doing it manually. How can you decide how large your bitmap should be and how many hashes you need?